(%i1) "Mathe Q1: Cornelsen, S. 114, Nr. 24"$


(%i2) "Funktionenschar untersuchen"$


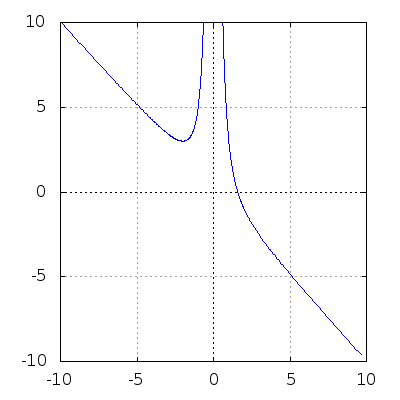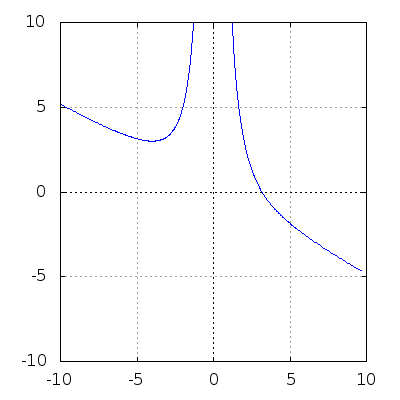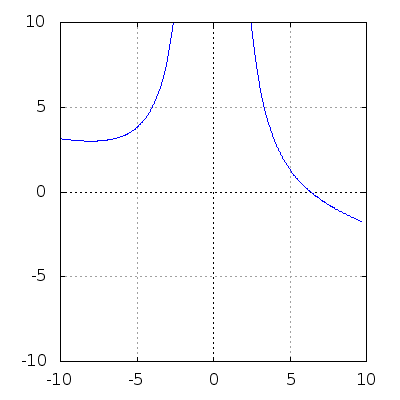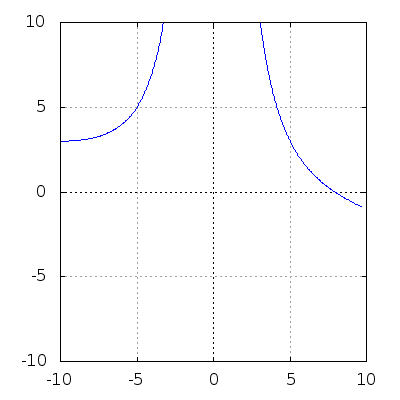
(%i3) f(x) := (4*k^3 - x^3)/(k*x^2);
                                          3    3
                                       4 k  - x
(%o3)                          f(x) := ---------
                                            2
                                         k x

(%i4) "Schnittpunkt mit y-Achse"$


(%i5) f(0);

expt: undefined: 0 to a negative exponent.
#0: f(x=0)
 -- an error. To debug this try: debugmode(true);

(%i6) "Nullstellen"$


(%i7) solve((4*k^3 - x^3)/(k*x^2)= 0, x);
                     1/3       1/3                     1/3       1/3
           (sqrt(3) 4    %i - 4   ) k        (sqrt(3) 4    %i + 4   ) k
(%o7) [x = --------------------------, x = - --------------------------, 
                       2                                 2
                                                                         1/3
                                                                    x = 4    k]

(%i8) ev(%,numer);
(%o8) [x = 0.5 (2.749459273997205 %i - 1.587401051968199) k, 
x = - 0.5 (2.749459273997205 %i + 1.587401051968199) k, 
x = 1.587401051968199 k]

(%i9) "1. Ableitung"$


(%i10) diff(f(x),x) ;
                                      3    3
                                2 (4 k  - x )   3
(%o10)                        - ------------- - -
                                       3        k
                                    k x

(%i11) sqfr(%);
                                     3      3
                                    x  + 8 k
(%o11)                            - ---------
                                         3
                                      k x

(%i12) "Mögliche Extremstellen"$


(%i13) solve( %th(2) = 0,x);
(%o13)    [x = (1 - sqrt(3) %i) k, x = (sqrt(3) %i + 1) k, x = - 2 k]

(%i14) ev(%,numer);
(%o14) [x = (1 - 1.732050807568877 %i) k, x = (1.732050807568877 %i + 1) k, 
                                                                     x = - 2 k]

(%i15) "2. Ableitung"$


(%i16) diff(f(x),x,2) ;
                                    3    3
                              6 (4 k  - x )    6
(%o16)                        ------------- + ---
                                     4        k x
                                  k x

(%i17) sqfr(%);
                                         2
                                     24 k
(%o17)                               -----
                                       4
                                      x

(%i18) "Mögliche Wendestellen"$


(%i19) solve( %th(2) = 0,x);
(%o19)                                []

(%i20) ev(%,numer);
(%o20)                                []

(%i21) "3. Ableitung"$


(%i22) diff(f(x),x,3) ;
                                     3    3
                              24 (4 k  - x )    24
(%o22)                      - -------------- - ----
                                      5           2
                                   k x         k x

(%i23) sqfr(%);
                                          2
                                      96 k
(%o23)                              - -----
                                        5
                                       x

(%i24) "Stammfunktion"$


(%i25) integrate(f(x), x);
                                     2      3
                                    x    4 k
                                  - -- - ----
                                    2     x
(%o25)                            -----------
                                       k

(%i26) sqfr(%);
                                     3      3
                                    x  + 8 k
(%o26)                            - ---------
                                      2 k x

(%i27) Funktionenschar für 1.0 <= k <= 5.0